组合数学知识点概括
明天下午组合数学考试,整理一些知识点,课本是:组合数学(第5版)卢开澄卢华明编著
第一章排列与组合
允许重复的组合 P20

线性方程组整数解个数 P21
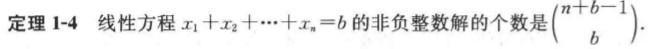
圆桌排列的公式,例题,下面的公式有误

例题2

字典序法,画树状图或者使用公式
数学归纳法证明题,例题

第二章递推关系和母函数
这里题型和内容比较难,需要多做题,熟悉各种题型(给出已知无穷序列求母函数,已知母函数求递推关系或是求它的第一二项a0、a1,递推关系等号右边等于0,递推关系等号右边等于常数,递推关系等号右边等于几的n次方的形式)
母函数定义 P46
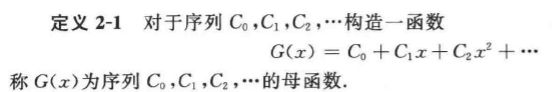
使用的泰勒公式 P47

线性常系数齐次递推关系 P55

三种:不同实数根、不同复数根、二重根
常系数非齐次递推关系 P62、 例题2-17,2-18 P65

第一第二类 Strling 公式 P102

常用性质:理解记忆(比如第六个性质的证明) P102

上面第六个性质的证明

第二类Strling数满足的递推关系 P103

第三章容斥原理和鸽巢原理
容斥原理:韦恩图,将这些集合的绝对值写出来,交集也写出来,然后画图。被整除的数的数目的注意要留下最小公约数,比如10000能被4和6整除的数的数目:10000/(46/2)=833(向下取整,floor(10000/(4\6/2))).
例题:

鸽巢原理:n+1只鸽子飞向n个鸽巢,一定存在两只鸽子飞向了同一个鸽巢。先划分好集合,可以按个位数、余数、奇偶数……
证明题很难,如:

棋盘多项式和有限制条件的排列 P130

一些可以手动推导的棋盘多项式 P130
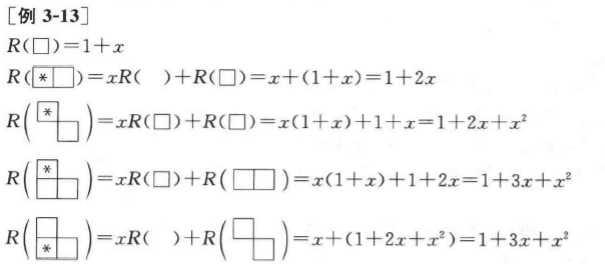
棋盘多项式的第四个公式:简化计算 P131

有禁区的排列

例如:,方案数是:3!-4*2!+4*1!-0!=1种
第四章Burnside引理和Poyla定理
前面群和域的概念很难理解
Poyla定理 P186

例题,不好理解:

第五章区组设计
拉丁方与正交拉丁方,构建正交拉丁方的过程(写出加法和乘法三线表,注意取余操作) P205

BIBD,均匀不完全的区组设计,记住两个公式

每个条件的首字母含义:
- b - Blocks(区组数):区组的总数。
- v - Varieties(处理数):实验中的不同处理种类数目。
- r - Repetition(重复次数):每个处理在所有区组中的出现次数。
- k - Keys(区组大小):每个区组中分配的处理数量。
- λ - Links(组合频率):每对处理组合在区组中共同出现的次数。
第一个公式代表元素出现的总和



