吴恩达机器学习
写的比较乱,对于一些不懂的问题都记录在下面了
一个人在不接触对方的情况下,通过一种特殊的方式,和对方进行一系列的问答.如果在相当长时间内,他无法根据这些问题判断对方是人还是计算机,那么就可以认为这个计算机是智能的.
——阿兰·图灵(Alan Turing)
《Computing Machinery and Intelligence 》
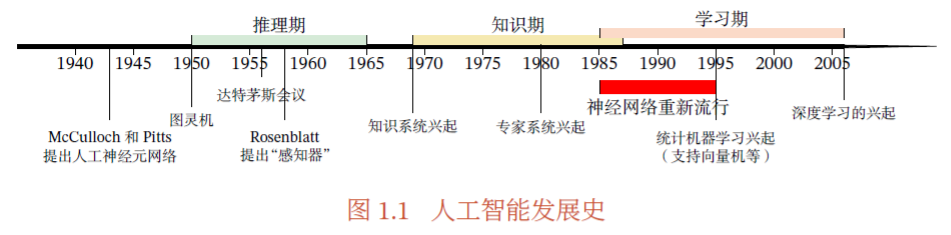
ps: 摘自 邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020. P5
代价函数
cost function,所有样本误差的平均,与损失函数不同的地方是,loss function是定义在单个样本上的误差。
常用的是平方误差代价函数
这里解释什么是代价,代价就是预测值与实际值之间的差距,对于多个样本来说就是代价之和,但是对于怎么处理这个和,有一定的门道,需要解决正负值、数据量与cost之间的关系,最终才采取了下面的函数
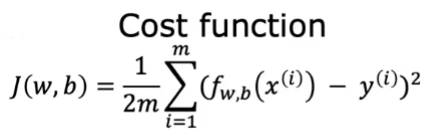
其中平方项可以抵消误差值正负数带来的影响,m是样本量,建立了代价(cost)与样本量之间的关系;1/2是为了在对w,b求偏导(partial derivative)可以简化式子。
https://www.cnblogs.com/geaozhang/p/11442343.html
判断梯度下降是否收敛
观察目标函数的损失函数值的变化情况,
- 梯度的范数:当梯度的范数趋近于零时,可以认为算法已经收敛。设置一个阈值。
- 目标函数值的变化
- 迭代次数,设置最大迭代次数
- 收敛曲线图,看图说话
激活函数
理解不了为什么要将输出变成非线性的,如何理解为什么需要激活函数?如果你串联几个线性变换,得到的最后依旧是一个线性变换,例如,f(x)=3x+1, g(x)=2x+2,串联这两个函数得到的是一个f(g(x))=6x+7,因此,如果在层之间没有一些非线性,那么即使是深层堆叠也等效于单层,你无法用它解决非常复杂的问题。相反,具有非线性激活的足够大的 DNN 在理论上可以逼近任何连续函数。(这种解释太帅啦,但是还是不能理解串联起来有什么用处,各个神经层次之间为什么需要串联以及串联和求导是什么关系)
- Sigmoid激活函数,也叫S形函数
ReLu函数
Tanh函数
Blog:https://www.cnblogs.com/XDU-Lakers/p/10557496.html
设置学习率
学习率Alpha,就是设置梯度下降的每一步的速率,不能过快也不能过慢
逻辑回归
没看懂
为了使反向传播正常工作,Rumelhart 和他的同事对 MLP 的架构进行了关键更改:他们用逻辑函数替换了阶跃函数,σ(z) = 1 / (1 + exp(–z)),也称为 S 形函数。
反向传播的工作原理
在 1970 年,一位名叫 Seppo Linnainmaa 的研究人员在他的硕士论文中介绍了一种自动高效计算所有梯度的技术。这个算法现在被称为反向模式自动微分(或简称反向模式自动微分)。通过网络的两次遍历(一次前向,一次后向),它能够计算神经网络中每个模型参数的误差梯度。换句话说,它可以找出如何调整每个连接权重和每个偏差以减少神经网络的误差。然后可以使用这些梯度执行梯度下降步骤。如果重复这个自动计算梯度和梯度下降步骤的过程,神经网络的误差将逐渐下降,直到最终达到最小值。这种反向模式自动微分和梯度下降的组合现在被称为反向传播(或简称反向传播)。
- 它一次处理一个小批量(例如,每个包含 32 个实例),并多次遍历整个训练集。每次遍历称为纪元。
- 每个小批量通过输入层进入网络。然后,算法计算小批量中每个实例的第一个隐藏层中所有神经元的输出。结果传递到下一层,计算其输出并传递到下一层,依此类推,直到得到最后一层的输出,即输出层。这是前向传递:它与进行预测完全相同,只是所有中间结果都被保留,因为它们需要用于反向传递。
- 接下来,算法测量网络的输出误差(即,使用比较期望输出和网络实际输出的损失函数,并返回一些误差度量)。
- 然后计算每个输出偏差和每个连接到输出层的连接对误差的贡献。这是通过应用链式法则(可能是微积分中最基本的规则)进行分析的,使得这一步骤快速而精确。
- 然后,算法测量每个下一层中每个连接贡献的误差量,再次使用链式法则,向后工作直到达到输入层。正如前面解释的那样,这个反向传递有效地测量了网络中所有连接权重和偏差的误差梯度,通过网络向后传播误差梯度(因此算法的名称)。
- 最后,算法执行梯度下降步骤,调整网络中所有连接权重,使用刚刚计算的误差梯度。
参考文章:https://www.cnblogs.com/apachecn/p/18006162
numpy dot versus matmul
import numpy as np
# Define two vectors for the dot product
vector_a = np.array([2, 3, 4])
vector_b = np.array([1, 5, 6])
# Calculate the dot product
dot_result = np.dot(vector_a, vector_b)
print(f"Dot Product: {dot_result}")
# Define two matrices for matrix multiplication
matrix_a = np.array([[1, 2, 3], [4, 5, 6]])
matrix_b = np.array([[7, 8], [9, 10], [11, 12]])
# Perform matrix multiplication
matmul_result = np.matmul(matrix_a, matrix_b)
print("Matrix Multiplication:")
print(matmul_result)result:
Dot Product: 41
Matrix Multiplication:
[[ 58 64]
[139 154]]
They serve different purposes and are used for distinct mathematical operations. np.dot() calculates the dot product between two arrays, whereas np.matmul() is specifically designed for matrix multiplication.
正则化、偏差和方差
正则化系数的选择
选择正则化系数λ 的值时也需要思考欠拟合和过拟合的问题。不知道如何理解正规化
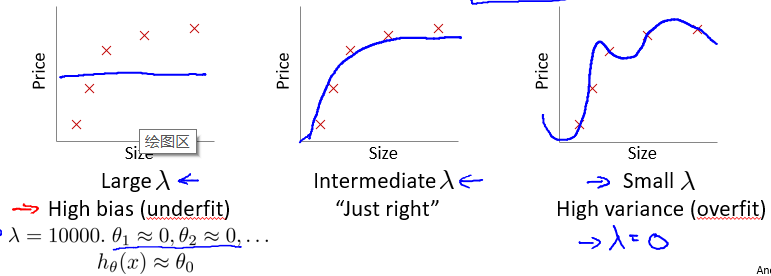
通常,我们选择一系列的想要测试的 λ 值,通常是 0-10 之间的呈现 2 倍关系的值(如:0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 共 12 个)。 我们同样把数据分为训练集、交叉验证集和测试集。
之后利用公式(看不懂公式):
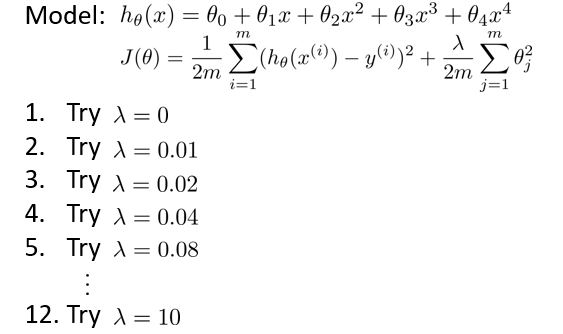
来选择λ,步骤是:
- 使用训练集训练12个不同程度的正则化的模型
- 用12个模型分别对交叉验证集计算出交叉验证误差,选择误差最小的模型
得出的结果图:https://momodel.github.io/mlbook/09/09-5.html
处理倾斜数据集
数据不平衡,比如处理不合格产品,合格率位96.4%,如果每次预测结果都是合格,准确率就可以达到96.4%,显然这种做法是不对的。
可以采用混淆矩阵来处理这种分类问题,对于给定的类别, 精确度和召回率的不同组合可以给出不同的意义,还可以使用ROC曲线来预测。
高质量回答:https://towardsdatascience.com/handling-imbalanced-datasets-in-machine-learning-7a0e84220f28
决策树
Decision Tree是一种解决分类问题的算法,监督学习主要有两种任务:分类(连续)、回归(离散)。
决策树算法采用树结构,层层推理来实现最终的分类。
决策树学习的三个步骤:特征选择、决策树生成、决策树剪枝(解决过拟合问题,随机森林很大程度减少过拟合)。
三种典型的决策树算法:ID3(采用信息增益)、C4.5(改进、采用信息增益比)、CART(采用基尼系数,CART树全称Classification And Regression Trees)
关于信息增益的理解:
熵:表示随机变量的不确定性
条件熵:在一个条件下、随机变量的不确定性能
信息增益:熵-条件熵,表示是在一个条件下,信息不确定性减少的程度。
详细解释:https://www.zhihu.com/question/22104055
One-Hot编码
独热编码,意思就是如果是相应编码位就是1,如果否相应编码位就是0,比如男女就可以用编码:01、10,再比如操作系统的采用位示图来表示磁盘中一个盘块的使用情况。
回归树
构建方式的核心:切分方式与属性选择
递归二分法
https://www.showmeai.tech/article-detail/192
How to understand clustering
这是一种非监督学习的算法(与classification最大的区别),将不同性质的数据分成几个相同类型的数据,如何评定相同类型的数据,可以有下面这些标准:Euclidean distance, Cosine similarity, Manhattan distance, etc.
聚类算法的分类:
- Centroid-based Clustering (Partitioning methods)
- Density-based Clustering (Model-based methods)
- Connectivity-based Clustering (Hierarchical clustering)
- Distribution-based Clustering
Clustering in Machine Learning - GeeksforGeeks
异常检测算法
找到与数据集分布不一致的算法,离群点、异常值检测
一般针对无监督异常检测,因为异常点常常是没有标签的
无监督异常检测算法的思想:
1、基于聚类的算法
2、基于统计的算法
3、基于深度的方法
4、基于分类模型
5、基于偏差的方法
6、基于重构的算法
7、基于神经网络的算法
丑小鸭定理
丑小鸭定理(Ugly Duckling Theorem)是1969 年由渡边慧提出的[Watanabe,1969].“丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大”.这个定理初看好像不符合常识,但是仔细思考后是非常有道理的.因为世界上不存在相似性的客观标准,一切相似性的标准都是主观的.如果从体型大小或外貌的角度来看,丑小鸭和白天鹅的区别大于两只白天鹅的区别;但是如果从基因的角度来看,丑小鸭与它父母的差别要小于它父母和其他白天鹅之间的差别.
这里的“丑小鸭”是指白天鹅的幼雏,而不是“丑陋的小鸭子”.渡边慧(1910~1993),美籍日本学者,理论物理学家,也是模式识别的最早研究者之一.
相似性的评定也需要主观标准,训练结果的相似性也要针对具体情况。
ps: 摘自 邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020.
超参数
超参数(Hyperparameter)是机器学习和深度学习中需要在训练模型之前设置的参数,而不是通过模型训练自动学习的参数。它们影响模型的训练过程和性能表现,通常需要通过实验和调优来选择最佳值。
超参数和模型参数的区别是:
- 模型参数:模型训练过程中从数据中学习得到的参数,例如线性回归中的权重或神经网络中的权重和偏置。
- 超参数:在训练之前设定的参数,决定了模型的结构和训练过程,如学习率、批量大小(batch size)、隐藏层的数量等。
常见的超参数包括:
- 学习率(Learning Rate):控制每次更新模型参数的步长。
- 批量大小(Batch Size):每次更新模型时使用的样本数量。
- 优化器类型(Optimizer):用于更新模型参数的方法,如SGD、Adam等。
- 正则化参数(Regularization Parameter):控制模型复杂度的参数,用于防止过拟合。
- 隐藏层数量和单元数量:对于神经网络,定义每层隐藏层的神经元数量和隐藏层的个数。
调优超参数通常通过交叉验证或网格搜索等技术进行,以找到模型性能的最佳配置。
梯度下降算法
在具体使用梯度下降法的过程中,主要有以下几种不同的变种,即:batch、mini-batch、Stochastic。其主要区别是不同的变形在训练数据的选择上。
批量梯度下降法(Batch Gradient Descent)针对的是整个数据集,通过对所有的样本的计算来求解梯度的方向。在每次迭代时需要计算每个样本上损失函数的梯度并求和。当训练集中的样本数量𝑁 很大时,空间复杂度比较高,每次迭代的计算开销也很大。
mini-batch GD:在上述的批梯度的方式中每次迭代都要使用到所有的样本,对于数据量特别大的情况,如大规模的机器学习应用,每次迭代求解所有样本需要花费大量的计算成本。是否可以在每次的迭代过程中利用部分样本代替所有的样本呢?基于这样的思想,便出现了mini-batch的概念。
BGD和SGD的对比:批量梯度下降法相当于是从真实数据分布中采集𝑁 个样本,并由它们计算出来的经验风险的梯度来近似期望风险的梯度.为了减少每次迭代的计算复杂度,我们也可以在每次迭代时只采集一个样本,计算这个样本损失函数的梯度并更新参数,即随机梯度下降法。在非凸优化问题中,随机梯度下降更容易逃离局部最优点。
SGD也有一些缺点,比如可能会导致收敛不稳定和收敛速度较慢。因此,许多研究者和工程师会使用 SGD 的变种,如 动量(Momentum)、Nesterov 加速梯度(Nesterov Accelerated Gradient)、Adam 等优化器,来克服这些缺点。
计算梯度的过程:在神经网络中,反向模式、前向模式都是都是应用链式法则的梯度累计方式,反向模式是更为有效的计算模式。在计算时,前向传播时会有一个计算图保存着所有操作节点的及其之间的关系,这样在反向传播计算梯度时(即调用backwrad函数),PyTorch 从损失函数(通常是计算图的最后一个节点)开始,沿着计算图向后遍历。在每个节点,PyTorch 会计算当前节点的输出对输入节点的导数(即梯度),并将这些梯度累加到每个输入的 .grad 属性中。
对于复合函数 的计算图如下:
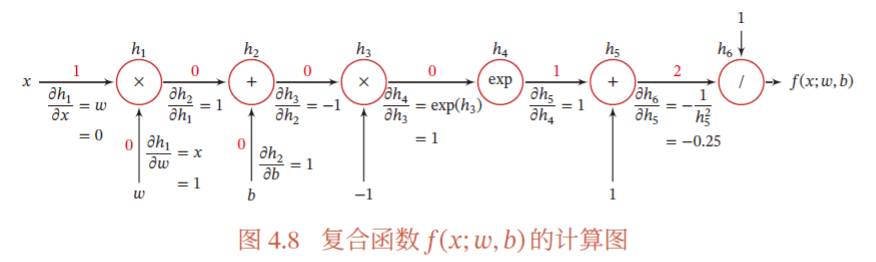
参考:邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020.
Blog:批梯度下降法(Batch Gradient Descent ),小批梯度下降 (Mini-Batch GD),随机梯度下降 (Stochastic GD),里面有几张非常形象的图片
非凸优化问题
在优化问题中,目标是找到使目标函数达到最小值或最大值的变量集。凸优化问题涉及的函数具有凸性质,即函数图像上的两点连线在函数图像的上方。这种情况下,局部最小值也是全局最小值,优化问题相对较为简单。然而,非凸优化问题涉及的函数图像可能出现上下凹凸,存在多个局部极小/大值,从而使问题变得复杂而有趣。
神经网络的三个概念:Batch、Epoch、Iteration
Batch表示批次,Iteration表示迭代,Epoch表示一代
Batch:batch_size将影响到模型的优化程度,选择batch_size是为了在内存效率和内存容量之间进行权衡,
batch_size选择总结:过小,训练数据会难以收敛,从而导致underfitting;增大,相对处理速度加快,所需内存容量增加。所以需要权衡,找到一个合适的batch_size。
Epoch:是指将全部的样本(所以的batch)都完成一次forward+一次backward,通常情况下,一个epoch是不够的,在多个epoch后,模型的weight和bias会逐渐的更新,达到理想状态。
Iteration:一个iteration包括了一个step中前向传播、损失计算、反向传播和参数更新的流程,有batch_size个iteration。
举个栗子:训练样本数量10000,batch_size=100,一共100个Batch,一个Batch有100个Iteration,一个Epoch有100个Barch的训练过程,但是在每个Batch都会去更新weight和bias。
参考:https://www.zhihu.com/question/43673341
梯度消失与梯度爆炸问题
问题产生的原因
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络.在循环神经网络中,神经元不但可以接受其他神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。
在RNN中,梯度计算时需要沿时间步反向传播(BPTT,Backpropagation Through Time),这个算法即按照时间的逆序将梯度信息一步步地往前传递.当输入序列比较长时了,时间步展开导致的长链乘积会存在梯度爆炸和消失问题,也称为长程依赖问题。
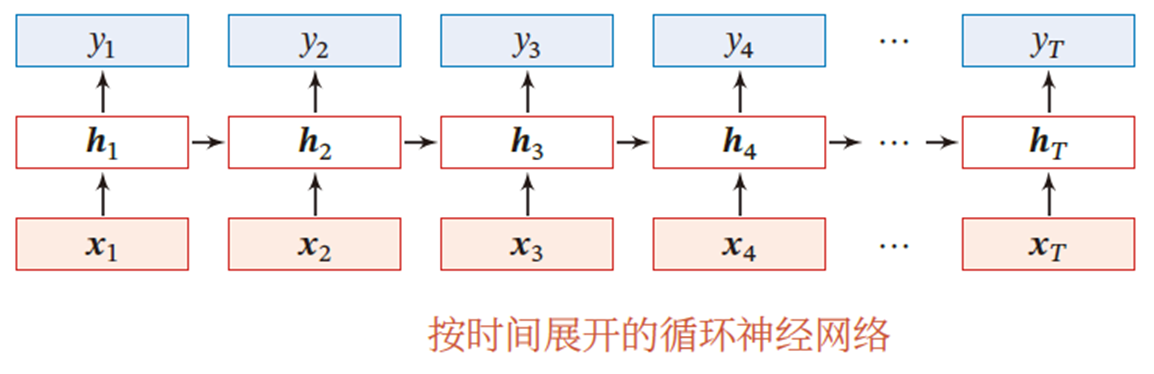
上图是一个简单的循环神经网络,只有一个隐藏层的神经网络, 不仅和当前时刻的输入 相关,也和上一个时刻的隐藏层状态相关
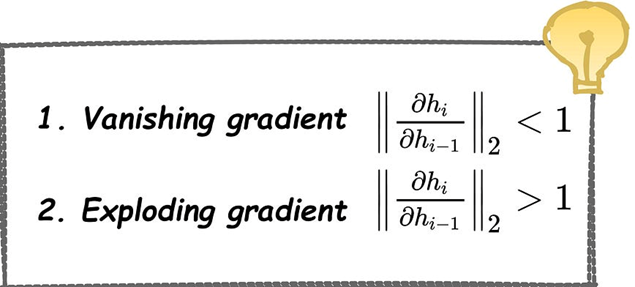
分析步骤

分析:
1、使用了一个4层的前馈神经网络来模拟展开的RNN。
2、若激活函数是Sigmoid,求梯度的最大值是0.25,可能会导致梯度消失问题,这时候网络就学习不到东西了,即无法更新梯度。
3、若权重设置过大了,可能出现梯度爆炸问题,梯度变成NaN。
注:最后等式括号中根据不同的激活函数有不同的导数。
Blog:
https://www.linkedin.com/advice/3/how-do-you-deal-vanishing-exploding-gradient
https://www.cnblogs.com/XDU-Lakers/p/10557496.html
https://www.cnblogs.com/imreW/p/17366268.html
https://www.cnblogs.com/zf-blog/p/12793019.html
总结
主要将平时遇到的问题来记录,并且加以补充和整理,参考了多本书籍,
如:邱锡鹏,神经网络与深度学习,机械工业出版社,https://nndl.github.io/, 2020.以及 艾伯特深度学习 中文版[aibbt.com]等
对于许多的博客中比较好理解的内容也进行了摘录(*\^_^*)
可忙,可闲,可急,可缓。
张弛之间,便是生活。






