数学基础
万丈高楼平地起
怎么说呢,学的数二对于这些东西还是太陌生了,而且当时学的只会做题,不知道怎么使用/(ㄒoㄒ)/~~
所以记下来一些不太清楚的前置知识点,主要来自《艾伯特深度学习》,书中内容很多,和《邱锡鹏神经网络与深度学习》内容有点相似
牛顿-莱布尼茨公式
揭示了定积分与被积函数的原函数或者不定积分之间的联系。
泰勒公式
以直代曲,一点一世界,数值越大高阶的作用越大,但是高阶的作用有时候过大了,所以采用阶乘来抵消一些作用,最终得到的效果就是更好的模拟曲线。
拉格朗日乘数法(乘子法)
求在约束条件下的极值。
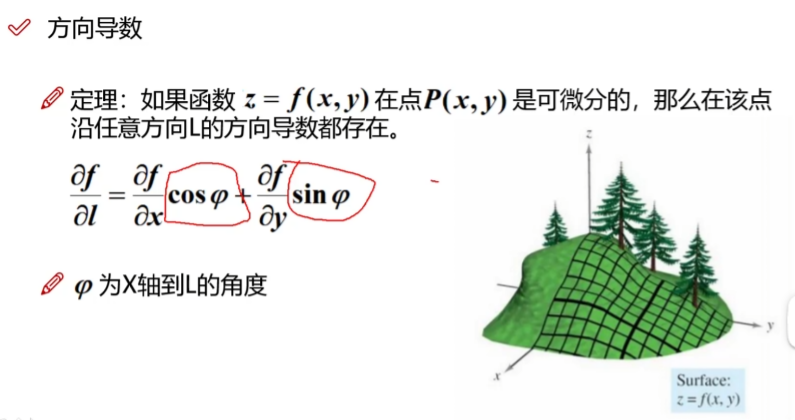
方向导数
fai 的角度大小要注意
梯度
蚂蚁跑离有火的地方,沿着梯度方向跑。梯度是一个向量,它的方向与方向导数最大值取得的方向一致。
概率与信息论的作用
概率论是用于表明不确定性申明的数学框架,提供的一种量化不确定性的方法,也提供了用于导出新的不确定性声明的公理。
概率可以被看作是用于处理不确定性的逻辑扩展。逻辑提供了一套形式化的规则,可以在给定某些命题是真或假的假设下,判断另外一些命题是真的还是假的。概率论提供了一套形式化的规则,可以在给定一些命题的似然后,计算其他命题为真的似然。
机器学习很多情况下需要处理不确定量,有时也需要处理随机量,随机性和不确定性来自于多方面,如建模系统内在的随机性、不完全观测、不完全建模等。
边缘概率
有时候,我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为边缘概率分布(marginal probability distribution)
协方差和标准差
常用概率分布
信息论
主要研究的是对一个信号携带信息量的多少进行量化。
方差
偏离期望值的程度的大小
大数定理
重复实验的次数越多,随机事件的概率越接近于它的概率。
马尔可夫不等式
将概率与期望建立联系,
范数
衡量向量的大小。当p = 2 时,L2 范数被称为欧几里得范数(Euclidean norm)。它表示从原点出发到向量x 确定的点的欧几里得距离。L2 范数在机器学习中出现地十分频繁。

特征值和特征向量
找特征向量的过程就是在找是否有一个矩阵左乘这个向量可以让它拉伸或者压缩。特征分解(eigendecomposition)是使用最广的矩阵分解之一,即我们将矩阵分解成一组特征向量和特征值。方阵A的特征向量(eigenvector)是指与A相乘后相当于对该向量进行缩放的非零向量v:
奇异值分解
还有另一种分解矩阵的方法,被称为奇异值分解(singular value decomposition,SVD),将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。
线代实例:主成分分析
PCA(principle components analysis),一个机器学习算法,可以通过线代的知识推导。见艾伯特深度学习2.12







